[자료구조] 자료구조

1. 자료구조 

자료구조란, 데이터 사이의 관계를 반영한 저장구조 및 그 조작 방법을 뜻한다. 컴퓨터의 프로그램을 실행하면 CPU에서 메모리로 데이터를 이동해서 처리하는데, 이 때 메모리를 효율적으로 사용하기 위해 데이터에 맞는 특성의 자료구조를 사용하는 것이 중요하다.

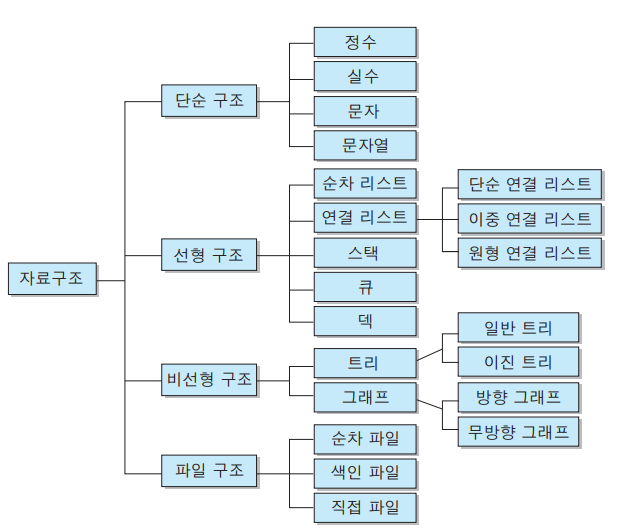
자료구조를 모두 나열하자면 아래 표와 같이 다양한 종류가 있다.

1.1 자료구조의 구성

• Insert : 데이터를 어떻게 저장 할 것인가
• Search : 데이터를 어떻게 탐색 할 것인가
• Delete : 데이터를 어떻게 삭제 할 것인가

1.2 자료구조의 분류

• 단순구조 : 프로그래밍에서 사용되는 기본 데이터 타입
• 선형구조 : 저장되는 자료의 전후관계가 1:1 (리스트, 스택, 큐 등)
• 비선형구조 : 데이터 항목 사이의 관계가 1:n 또는 n:m (트리, 그래프 등)
• 파일구조 : 서로 관련된 필드들로 구성된 레코드의 집합인 파일에 대한 자료구조

---

2. 선형자료 구조

2.1 배열

파이썬에서는 그냥 리스트 자료구조를 사용한다.

array1 = [] # 빈 리스트.
array2 = [0, 1, 2, 3, 4] # 길이가 5인 리스트. C언어나 파이썬은 숫자를 0부터 센다.
array3 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] # 리스트 안에 리스트가 중첩되어 있다.
# 리스트 안에는 리스트를 포함하여 어떤 객체도 넣을 수 있다.

자바에서는 대괄호의 위치가 변수명보다 앞에 있다.

int[] array1;
int[] array2 = new int[10]; //heap 메모리에 할당하여 사용
int[] array3 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; //C언어와 동일한 초기

2.2 해시

Key와 Value가 쌍을 이루는 자료구조로 해시는 해시 함수로 구현한다. 해시 함수는 마치 배열처럼, 어떤 자료를 찾을 때 O(1)의 시간만을 소요한다. 해시함수에 키 값을 넣어 주소값을 얻고, 그 주소에 위치한 버킷에 저장된 데이터를 가져오는 방식을 사용한다. 하지만, 언제나 O(1)이 보장되는 것은 아니다.

 

파이썬의 해시는 “딕셔너리”(Dictionary)라고 부른다.

dict1 = {1:"하나", "apple":"사과", "리스트":[1, 2, 3]}

String str = "hello";
int hashCode = str.hashCode();
System.out.println(hashCode);

ArrayList는 내부 인덱스를 이용하여 검색이 한번에 이루어지기 때문에 빠른 검색 속도를 보장하는 반면 데이터의 추가/삭제시 많은 데이터가 밀리거나 당겨지기 때문에 많은 시간이 소요된다.
LinkedList는 추가/삭제시 인근 노드들의 참조값만 수정해 줌으로써 빠른 처리가 가능하지만 데이터를 검색할 경우 해당 노드를 찾기 위해 처음부터 순회 검색을 해야하기 때문에 데이터의 수가 많아질수록 효율이 떨어지는 구조이다.
*이러한 한계를 극복하기 위해서 제시된 방법이 Hash이다.

2.3 스택

먼저 들어간 자료가 나중에 나오는 자료구조. 유식한 말로 후입선출(後入先出) 구조라고 한다. 자료를 넣는 push 함수와 자료를 빼는 pop 함수를 갖는 게 정석이다. empty, full 등 다른 함수들을 가질 수 있다. C++의 STL에서 지원한다.

자바의 배열 자료구조로 스택 클래스를 만들면 다음과 같을 것이다. C언어와 동일한 기능을 수행하도록 구현하였다.

public class Stack{
    int size = 500;
    int[] arr = new int[size];
    int top = 0;
    
    int push(int n){
        if(top > size){
          return -1;
        }
        arr[top++]=n;
        return 0;
    }
 
    int pop(){
       if(top <= 0){
         return -1;
       }
       return arr[--top];
    }
 
    public static void main(String[] args){
      Stack stack = new Stack();
      stack.push(1);
      stack.push(2);
      stack.push(3);
      System.out.printf("%d %d %d", stack.pop(), stack.pop(), stack.pop());
    }
}

2.4 큐

먼저 들어간 자료가 먼저 나오는 자료구조. 선입선출(先入先出) 구조라고도 한다. 자료를 넣는 Enqueue 함수와 자료를 빼내는 Dequeue 함수를 가진다.

밑의 큐는 연결 리스트로 구현된 큐이다. 배열로 하는 경우에는 보통 순환 큐라고 해서 맨 끝과 앞을 연결(나머지 연산자 % 이용)하는 방식으로 구현한다. 

자바에서 연결 리스트 자료구조로 큐를 구현하는 클래스를 작성 하자면 다음과 같을 것이다.

import java.util.Queue;

public class Queue {

    Queue<Integer> queue = new LinkedList<>();

    void enQueue(int n){
        queue.add(n);
    }

    int deQueue(){
        return queue.poll();
    }
}

2.5 링크드 리스트

연결 리스트라고도 불린다.

값과 다음 노드를 가지고 있다. 옵션으로 이전 노드를 가지게 할 수도 있으며, 맨 뒤 노드가 맨 앞 노드를 다음 노드로 가지게 할 수도 있다. 또한, 중간에서 삽입과 삭제를 할 수 있다. 가장 간단하게 구현한 것은 위의 큐. 다시 한 번 뜯어보고 옵션을 넣어본다면 실력 향상에 도움이 될 것이다. 다만, 링크드 리스트는 원소들이 이곳저곳에 흩어져있어서 구현체의 속도가 느리기 때문에, 잘 사용되지는 않는 편이다.

---

3. 선형구조 자료 탐색법

말 그대로 선형구조로 된 자료를 탐색하는 방법이다. 보통 어떤 값이 어디에 있는지 알아내는 게 목적이다.

3.1 순차 탐색

말 그대로 시작점부터 순차적으로 탐색하는 것이다. 전부 탐색한다고 생각할 때,연산량은 O(n)이다.
솔직히 이건 해당 언어만 알면 누구나 코드를 만들어낼 수 있을 수준이기에,소스 코드 부분은 생략한다.

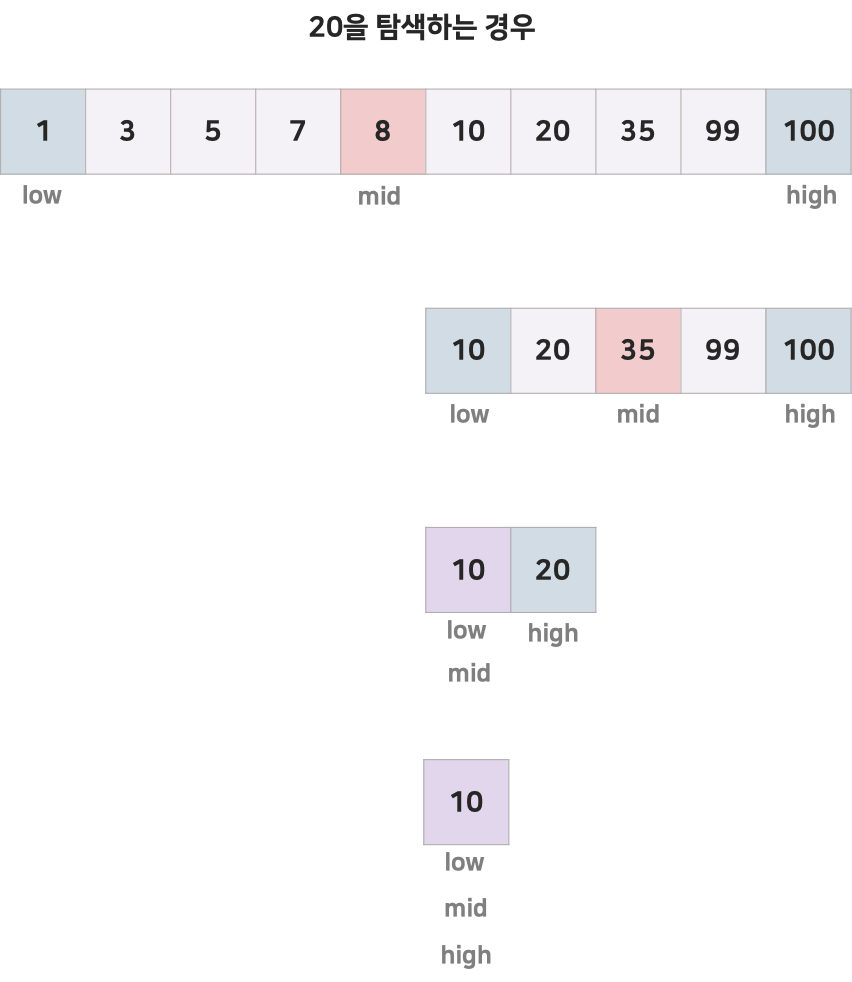
3.2 이분 탐색 (Binary Search)

특수한 상황에서 순차 탐색보다 좀 더 빠른 속도를 기대할 수 있는 알고리즘으로,연산량은 O(log2 N)이다. 이분 탐색이란, 순차 탐색과 달리 가운데에서 시작해서 매번 일정한 조건에 따라 어떤 방향의 가운데 값으로 탐색할 지 결정하는 알고리즘이다.이 때 가운데 값이란 평균이 아니고 중간값이다.

이를 좀 더 자세히 설명하자면 이렇다. 배열 1 3 4 7 8 13 17에서 '8'이 있는 위치를 찾는다고 가정하자.

배열: 1 3 4 7 8 13 17
1st:총 배열의 가운데인 7을 선택.
7<8 이므로 더 큰 숫자가 있는 오른쪽으로 진행.
2nd:7~17의 배열중 가운데인 13을 선택.
13>8 이므로 더 작은 숫자가 있는 왼쪽으로 진행.
3rd:7과 13의 가운데에 있는 8을 선택.
8=8 이고 배열은 5번째이므로 답은 5이다.

 

단,이를 위해서는 특수한 기준으로 정렬되어 있어야 한다. 

건복치님의 이진 탐색의 구현 참고 

1. 탐색의 대상이 되는 자료들이 array[low] 에서부터 array[high]에 들어있다고 가정하자. (정렬되어 있어야 함)

2. low와 high값에 의거해  중간값 mid 값은 (low + high) / 2이다.

3. array[mid] 값과 구하고자 하는 key값을 비교한다.

3-1. key > mid :  구하고자 하는 값이 중간값보다 높다면 low를 mid +1로 만들어 줌 (왼쪽 반을 버림)

3-2. key < mid : 구하고자하는 값이 중간값 보다 낮다면 high를 mid-1로 만들어 줌 (오른쪽 반을 버림)

3-3. key == mid : 구하고자 하는 값을 찾음 중간값 리턴 

4. low > high가 될 때까지 1~3번을 반복하면서 구하고자 하는 값을 찾는다.

▶  순환 호출을 이용한 이진 탐색 구현

▶  반복을 이용한 이진 탐색 구현 

반복 구조를 사용하는 것이 재귀 호출로 구현하는 것보다 효율적이다.

public class BinarySearch {
	static int[] arr = {1, 3, 5, 7, 8, 10, 20, 35, 99, 100};

	public static void main(String[] args) {
		System.out.println("1. 순환 호출을 이용한 이진 탐색");
		System.out.println(binarySearch1(5, 0, arr.length-1)); // 2
		
		System.out.println("\n2. 반복을 이용한 이진 탐색");
		System.out.println(binarySearch2(20, 0, arr.length-1)); // 6
		
	}
	
	// 재귀적 탐색
	static int binarySearch1(int key, int low, int high) {
		int mid;
		
		if(low <= high) {
			mid = (low + high) / 2;
			
			if(key == arr[mid]) { // 탐색 성공 
				return mid;
			} else if(key < arr[mid]) {
				return binarySearch1(key ,low, mid-1); // 왼쪽 부분 탐색 
			} else {
				return binarySearch1(key, mid+1, high); // 오른쪽 부분 탐색 
			}
		}
		
		return -1; // 탐색 실패 
	}
	
	// 반복적 탐색
	static int binarySearch2(int key, int low, int high) {
		int mid;
		
		while(low <= high) {
			mid = (low + high) / 2;
			
			if(key == arr[mid]) {
				return mid;
			} else if(key < arr[mid]) {
				high = mid - 1;
			} else {
				low = mid + 1;
			}
		}
		
		return -1; // 탐색 실패 
	}

}

// 재귀적 탐색
/헤더 부분
int solve(int,int);
//소스 부분
int A[500]; //총 500개까지 담을 수 있는 배열에서 탐색.
int k; //탐색할 값.

int solve(int s, int e);
{
    int m;
    while(e-s>=0)
    {
        m=(s+e)/2; //값이 있을 가능성이 있는 값의 가운데 값.
        if(A[m]==k)
            return m+1; //그 값이 만약 탐색할 값이면 그 위치를 리턴.
        if(A[m]<k) s=m+1; //만약 A[m]이 작으면 좀 더 큰 값들이 있는 오른쪽이 탐색되도록 변경.
        else e=m-1; //아까와 정반대.
    }
    return -1; //찾는 값이 없을 경우 -1을 준다.
}

---

4. 비선형 자료구조

선형 자료구조가 아닌 모든 자료구조이다. 다만,사전적인 정의를 하자면 i 번째 값을 탐색한 뒤의 i+1이 정해지지 않은 구조를 의미한다.

4.1 그래프

함수의 그래프와는 전혀 다르다. 알고리즘을 배우다 보면 자주 나오는 구조로, 점들, 그리고 점들을 연결하는 선들만으로 이루어진 지도 비스무리한 걸 연상하면 편하다. 이때의 점을 정점(vertex), 선을 간선(edge)이라고 부른다.[7]

간단한 구조체를 하나 살펴보자.  struct Edge가 하나 이상 있는 것이 바로 그래프이다.

struct Edge //정점보다는 간선으로 나타내는 편이 대부분의 경우에 더 좋다.
{
    int snode; //시작 정점
    int enode; //종료 정점
    //int cost; //가중치를 가지는 간선에 사용된다.
};

▶ 그래프 관련 용어

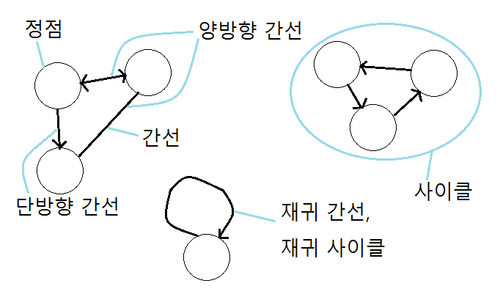
1. 정점(Vertex) : 간단하게 말해서, 연결점이다. 좀 더 구체적으로 정의하자면, 여러 가지 특성을 가질 수 있는 객체이다. 즉, 어떤 객체도 정점이 될 수 있다.
   1-1. 고립 정점 : 간선이 단 하나도 연결되지 않은 외톨이 정점이다.
2. 간선(Edge) : 두 정점을 연결하는 연결선이다. 구체적으로는, 두 정점간의 관계이다.
   2-1. 단방향 간선 : 단방향으로만 이동 가능한 간선이다. 이동이 가능한 방향으로 화살표를 그린다.
   2-2. 양방향 간선 : 양 방향으로 모두 이동이 가능한 간선이다. 양쪽 화살표를 사용해도 되지만, 양방향 그래프에서는 모든 간선이 양방향 간선이므로 화살표 대신 선분으로 표현하기도 한다.
   2-3. 자기 간선 : 자기 자신을 연결하는 간선이다.
   2-4. 다중 간선 : 동일한 다른 접점과 여러 간선이 연결되는 간선이다.
   
3. 인접 : 두 정점이 하나의 간선으로 연결되어 있을 때 두 정점이 인접하다고 한다.
4. 치수(Degree) : 정점에 연결된 간선의 수이다.
5. 경로(Path) : 어떤 한 정점에서 다른 하나의 정점으로 가는 길이다. 두 정점이 반드시 다를 필요는 없다.
6. 부분 그래프 (Sub Graph) : 그래프를 구성하는 정점들을 임의로 선택한 후 그 정점을 연결했던 간선들로 선택한 정점을 연결한 그래프를 말한다.

1.  

▶  그래프의 종류

그래프일반적인 정의는 객체들 사이의 관계를 점과 선으로 나타낸 그림이다. 그래프는 크게 두 구성요소 정점과 간선으로 이루어져 있다.

1. 단순 그래프 : 임의의 두 정점 사이에 간선이 최대 하나 있는 그래프
2. 다중 그래프 : 임의의 두 정점 사이에 여러 개의 간선을 허용하는 그래프
3. 의사 그래프 : 다중 그래프이면서 사이클을 허용하는 그래프
4. 양방향(무향) 그래프 : 연결된 두 정점의 순서를 바꾸어도 같은 간선이 되는 그래프, 즉 양방향으로 통행이 가능한 그래프
5. 단방향(유향) 그래프 : 일방통행만 가능한 그래프.
6. 연결 그래프 : 임의의 두 정점 사이에 반드시 경로가 존재하는 그래프.
   완전 그래프 - 모든 정점이 서로 간선으로 양방향 연결되어 있는 그래프
7. 가중치 그래프 : 간선에 가중치가 부여된 그래프

▶ 그래프 순회 알고리즘

그래프를 순회하는 방법이다. 각 방법마다 장단점이 있으니 상황에 따라 적절한 알고리즘을 선택하는 것이 중요하다.

▶  깊이 우선 탐색 (DFS)

Depth First Search, DFS라고 불리며, 구현하기 쉬운 알고리즘 중 하나이다. 이름 그대로, 방문한 정점으로부터 깊게 들어가며 쭉 탐색한 후, 되돌아 나오다가 아직 탐색하지 않은 노드를 탐색하는 방식을 사용한다.

알고리즘의 실행과정을 설명하면 다음과 같다.

1. 첫 정점을 방문한다.
2. 인접한 정점 중 아직 방문하지 않은 정점을 방문한다(한 길로 쭉 파고 들어간다).
3. 더 이상 들어갈 길이 없을 때(인접한 모든 정점이 이미 방문한 정점일 때), 방문하지 않은 인접한 정점을 찾을 때까지 들어간 길을 돌아나온다.
4. 위 과정을 반복한다.

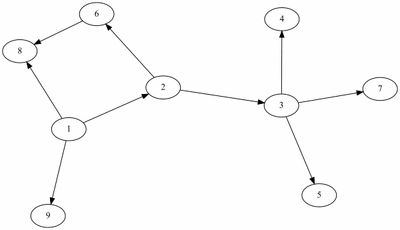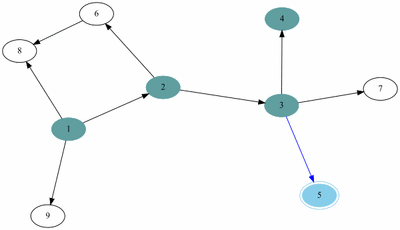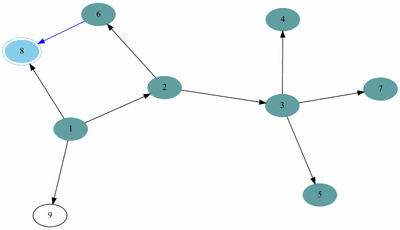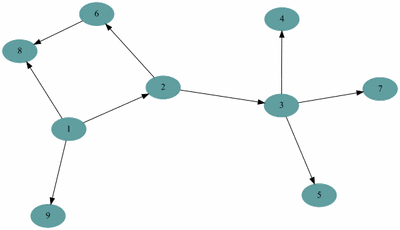
여기서 DFS를 구현하는 함수의 모양은 다음과 같다. 단,그래프는 인접리스트를 활용했다고 가정한다.

예제(그림)의 경우 방문 순서는 1, 2, 3, 4, 5, 7, 6, 8, 9 이다.

여기서 DFS는 깊이가 너무 큰 경우, 런타임 에러를 뿜는다는 단점이 있다.

▶  너비 우선 탐색 (BFS)

Breadth First Search, BFS라고 불린다. 이름 그대로, 넓게 퍼져가며 정점을 방문한다.

알고리즘의 실행과정은 다음과 같다.

1. 첫 정점을 방문한다.
2. 아직 방문하지 않은 인접한 정점들을 큐에 넣는다.
3. 큐에 있는 정점들을 순서대로 방문한다.
4. 큐에 있는 정점에 대해 인접하면서 아직 방문하지 않은 정점들로 새로운 큐를 구성한다.
5. 위 과정을 반복한다.

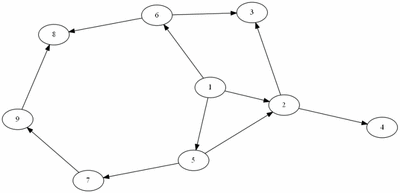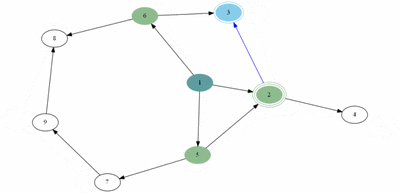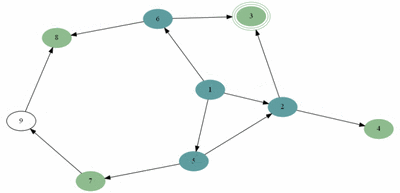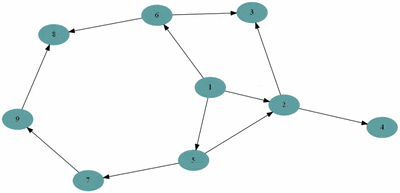
예제(그림)의 경우 방문 순서는 1, 2, 5, 6, 3, 4, 7, 8, 9 이다.

4.2 트리

그래프의 일종이다. 트리에서의 정점을 특별히 노드라고 하고, 간선을 특별히 가지라고 한다.

▶  트리 관련 용어

1. 노드(Node) : 그래프의 정점에 해당하는 것이다.
   
   1. 루트 노드 : 트리의 기준이 되는 노드이다. 나무의 뿌리를 생각하면 된다. 루트 노드 위에 가지가 뻗어 있다는 이미지.
   2. 부모 노드 : 어떤 노드에서 자신과 인접한 노드들 중 루트 노드로 향하는 노드.
   3. 자식 노드 : 어떤 노드에서 자신과 인접한 노드들 중 루트 노드의 반대 방향으로 향하는 노드.
   4. 단말 노드 : 자식 노드가 존재하지 않는 노드. 가지의 끝이라고 생각하면 된다.
   5. 형제 노드 : 부모 노드가 같은 노드.
2. 가지(Branch) : 그래프의 간선에 해당하는 것이다. 트리에서는 양방향 간선만 사용한다.
3. 부트리(Sub Tree) : 부분 그래프와 비슷하게 정의한다.
4. 차수(Degree) : 자식 노드의 개수.
5. 길이(Length) : 임의의 두 노드를 시작 노드, 도착 노드로 하는 경로에서 거치게 되는 노드의 수.
6. 깊이(Depth) : 루트 노드에서 해당 노드까지의 길이.
7. 레벨(Level) : 깊이가 같은 노드의 집합.
8. 높이(Height) : 가장 깊이가 깊은 단말 노드까지의 길이.

▶  트리의 종류

1. 이진 트리 : 모든 노드의 차수가 2 이하인 트리.
2. 전 이진 트리 : 모든 노드의 차수가 0 또는 2인 트리.
3. 포화 이진 트리 : 모든 단말 노드의 깊이가 같은 이진 트리.
4. 완전 이진 트리 : 모든 단말 노드의 깊이의 최댓값과 최솟값의 차이가 0 또는 1인 이진 트리.

▶  트리 순회 알고리즘

트리를 순회하는 방법이다.

▶  전위 순회

그래프에서의 깊이 우선 탐색과 같다.

▶  중위 순회

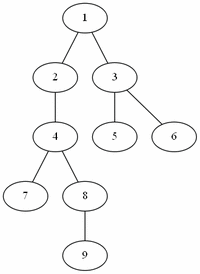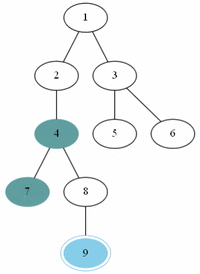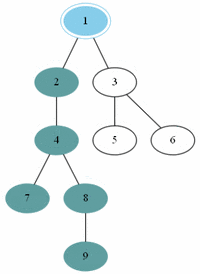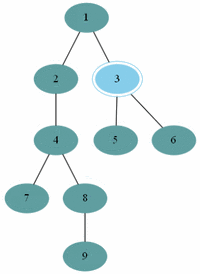
이진 트리에서만 할 수 있는 순회 알고리즘이다.

▶  후위 순회

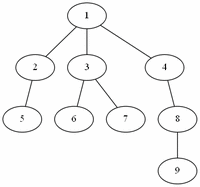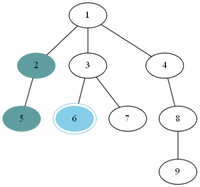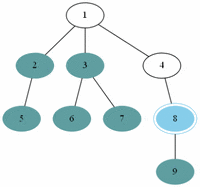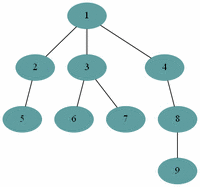
▶  레벨 순서 순회

그래프에서의 너비 우선 탐색과 같다. 

▶ 이진 검색 트리

이진 검색은 일자로 나열된 정렬된 데이터에서 원하는 데이터를 빠르게 찾는 방법이다. 최악의 경우에 O(log n)를 보장하는 매우 유용한 알고리즘이다. 정렬의 중요성은 거의 이 알고리즘을 통한 활용에 있다고 할 수 있다. 이진 검색 트리는 이진 검색에 용이하게 데이터를 다음과 같은 방법으로 이진트리로 구성한 것을 말한다.

1. 일렬로 나열된 데이터들 중 가장 중앙에 위치한 하나의 데이터를 M이라고 하고, M 왼쪽에 위치한 데이터들을 L, 오른쪽에 위치한 데이터를 R이라 하자.
2. L과 R이 M을 부모로 가지는 트리를 구성한다.
3. L과 R에 대해서도 각각 같은 방법으로 트리를 구성한다.

▶ 이진 검색

이분 탐색과 동일한 알고리즘이다. 여기에서는 트리라는 특징을 중점으로 해서 설명한다. 오름차순 정렬된 자료를 기준으로 한다. 이진 검색 트리의 루트 노드부터 방문하며, 다음 순서에 따라 노드를 방문한다.

---

연관된 글 :

[알고리즘] 깊이우선탐색(DFS)과 너비우선탐색(BFS)

알고리즘 공부 시작하기 (참고 사이트)

[알고리즘] 시간 복잡도

코딩테스트 자주 사용하는 코드 for JAVA

 

참고 :

자료구조 - 스택, 큐 직접 구현(Stack, Queue)

[자료구조] 스택(Stack)이란

초보몽키의 개발공부로그

[JAVA] Hash란 무엇인가?

시리즈:수학인듯 과학아닌 공학같은 컴퓨터과학/알고리즘 기초

[Algorithm] 알고리즘 공부 시작 방법 및 순서

알고리즘 - 자료구조(1) 스택, 큐

건복치님의 이진 탐색의 구현 참고